벨만포드 알고리즘

  • 2022/06/01
  • 3-minute read

참고 원본 - 벨만포드 알고리즘 7분 요약

BOJ 11657 타임머신 문제

Table of Contents

최단 거리 문제

  • 그래프에서 최단 거리를 찾는 문제
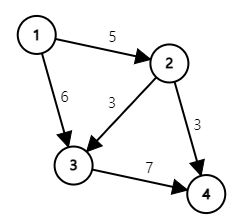
  • 일반적으로 최단 거리 문제에서 자주 사용하는 알고리즘은 다익스트라 알고리즘 Shortest_path

다익스트라 알고리즘

  • 다익스트라 알고리즘
  • 다이나믹 프로그래밍을 활용하는 알고리즘
  • 특정한 하나의 Node에서 다른 모든 Node로의 최단 거리를 계산하는 알고리즘
  • 각 Node 사이의 Edge가 양수일 때 사용할 수 있음
  • 현실 세계와 잘 맞아 떨어지므로, 현실 세계에 사용하기 적합한 알고리즘

Negative Edge?

  • 현실에 존재하는 일반적인 상황이 아닌 경우 Edge의 값이 음수인 경우가 존재
  • 이와 같은 경우에는 다익스트라 알고리즘을 적용하여 계산이 불가능
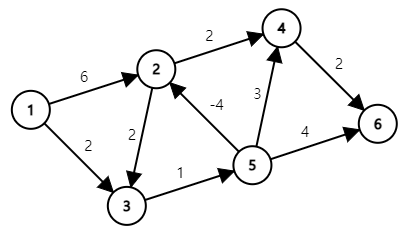
  • 또한, 발생한 사이클 내부의 Edge 값의 합이 음수인 경우, 최단 거리가 모두 $-\infty$가 될 수 있음 Negative_Cycle
  • 이에 따라, 음수인 Edge를 포함한 그래프의 최단 거리를 구하는 알고리즘과 사이클의 합이 음수가 되는지를 확인하는 알고리즘이 모두 필요

Bellman-Ford Algorithm

  • 이와 같은 음의 Edge를 포함하는 경우 및 사이클의 합이 음수가 되는지를 파악하는 알고리즘이 벨만포드 알고리즘
  • 모든 Edge에 대해 확인하므로, 다익스트라 알고리즘보다 속도가 느림
  • 시간 복잡도는 $O(VE)$, $V \rightarrow$ Node 개수, $E \rightarrow$ Edge 개수
  1. 출발 Node를 설정
  2. 최단 거리 테이블을 초기화 (출발 Node는 0, 나머지는 모두 무한대 ($1e9$))
  3. 아래의 과정을 $N-1$번 반복
    • Edge $E$개를 모두 확인
    • 각 Edge를 거쳐서 다른 Node로 가는 비용을 계산해서 최단 거리 테이블을 업데이트
  4. 음수 Edge 순환 여부를 판단하려면, 3의 과정을 1번 더 수행하여, 최단 거리 테이블이 업데이트되면, 순환이 존재하는 것으로 판단

벨만포드 vs 다익스트라

  • 다익스트라
    • 방문하지 않은 Node 중에 최단 거리가 가장 짧은 Node를 선택하여 해당 Node를 경유한 경로를 통해 최단 거리 테이블을 업데이트
    • 음수 Edge가 없다면 최적해를 찾을 수 있음
  • 벨만포드
    • 매번 모든 Edge를 확인 $\rightarrow$ 다익스트라의 최적해를 항상 포함할 수 밖에 없음
    • 시간은 다익스트라보다 오래 걸림
    • 음수 Edge가 포함된 경우의 최단 거리 계산 및 음수 Edge 사이클 탐지가 가능

구현 Tip

  • 벨만포드 구현 시, 알고리즘 상으로는 $N-1$번 탐색하지만, $N$번 탐색하는 방법을 통해, 사이클 탐지도 함께 확인할 수 있음
def bellman_ford(start, dist_table, N, M, edges):
    dist_table[start] = 0 # 시작 Node의 거리 초기화
    for i in range(N): # N-1대신 N번 탐색을 통해 사이클도 함께 탐지
        for j in range(M): # 모든 Edge를 탐색
            cur = edges[j][0] # edges는 (시작 Node, 도착 Node, 비용)이 저장되어 있음
            target = edges[j][1]
            cost = edges[j][2]
            if dist_table[cur] != INF and dist_table[target] > dist_table(cur) + cost: # 현재 Edge를 통해 이동하는 경우가 더 짧은 경우
                dist_table[target] = dist_table[cur] + cost
                if i == N - 1:
                    return True # N번째 확인 시에, 값이 업데이트 되면 음의 사이클 확인
    return False # N번째 확인 시에, 값이 업데이트 되지 않았으므로, 음의 사이클 없음

Review

  • 그냥 봤을 때 느낌으로는 전체 경우의 수를 다 찾는 느낌이라, 브루트 포스 느낌이 들었는데 그런진 모르겠다
  • 다익스트라랑 비슷한 느낌이라 이해하기가 어렵진 않았다
  • 음의 간선이라는 문제가 이해가 안됐는데, 타임머신ㅋㅋ….

comments