A* 알고리즘
-
2022/06/03
-
13-minute read
Table of Contents
개요
- 길 찾기 알고리즘은 꽤나 많은 영역에서 사용됩니다.
- 대표적으로 게임 내부에서의 길 찾기가 있습니다.
- 길을 찾을 때는 최단 경로도 중요하지만, 비용도 고려해야합니다.
- 아래와 같은 지도에서 시작 위치부터 도착 위치까지의 경로를 찾는 방법은 Graph 탐색 알고리즘이 있습니다.
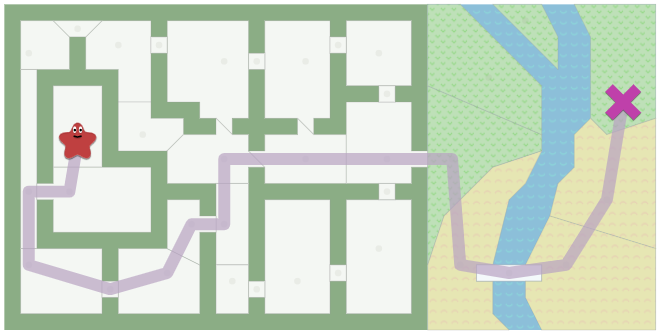
- 가장 쉬운 방법은 BFS 알고리즘입니다.
- 대중적으로는
A*를 많이 사용하고 있습니다.
지도 표현하기
- 길 찾기를 수행하기 전에 중요한 점 중 하나는 입력과 출력을 확인하는 것입니다.
- 입력으로 Graph가 들어온다면,
A* 또는 BFS를 사용할 수 있씁니다.
- Graph는 여러 개의 위치(Node)와 그 사이의 연결선(Edge)을 포함하고 있습니다.
- 아래와 같은 Graph를
A*의 입력으로 주겠습니다.
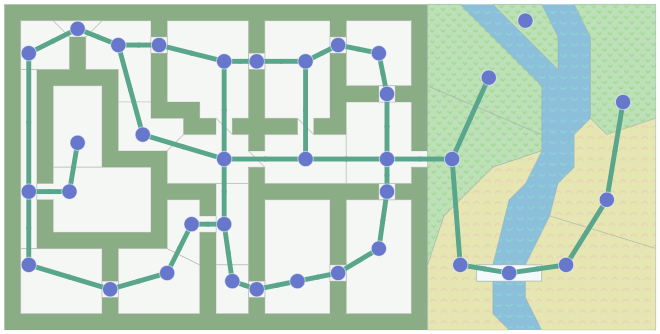
A*는 Graph 그 자체만을 확인합니다.- 그 외의 것들, 실내 or 실외, 복도 or 방의 내부, 공간의 크기 등에 대해서는 신경쓰지 않습니다.
- 예를 들어 아래와 같은 입력이 들어와도, 위의 입력과 동일하다는 의미입니다.
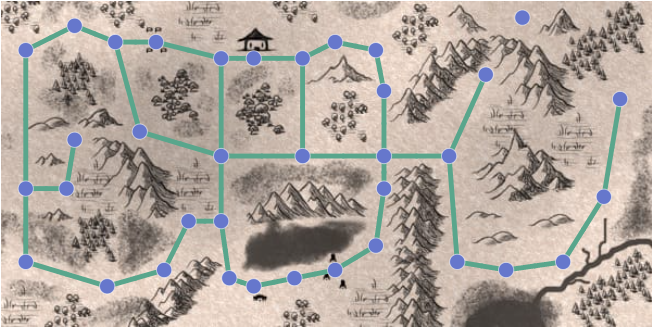
- 이에 대한 출력은
A*의 결과로 나온 Node와 Edge로 이루어진 경로입니다.
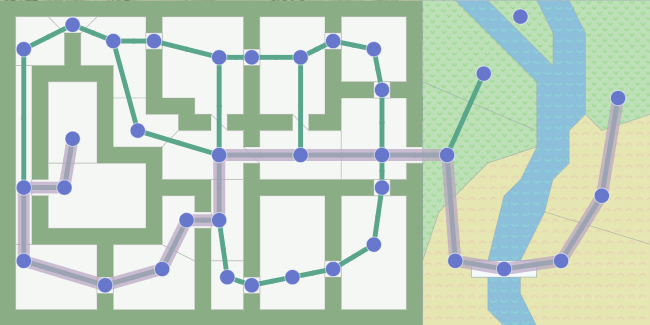
A*는 이동해야할 위치를 알려주지만, 어떻게 이동하는지는 알려주지 않습니다.- 그 이유는
A*는 Graph 이외의 정보에 대해 모르기 때문입니다.
- 따라서 사용자는
A*의 결과를 타일와 타일 사이처럼 이동할 지, 직선으로 이동할 지, 문을 열지, 수영을 할지, 커브 길을 따라 달려갈지 등을 결정해야합니다.
- 어떤 게임 지도에서도,
A*에 넘겨줄 수 있는 Graph를 만드는 방법이 다양합니다.
- 위의 지도는 대부분의 출입구를 Node에 포함시켰습니다.
- 하지만 모든 출입구를 넣는다면 Graph는 아래와 같을 것입니다.
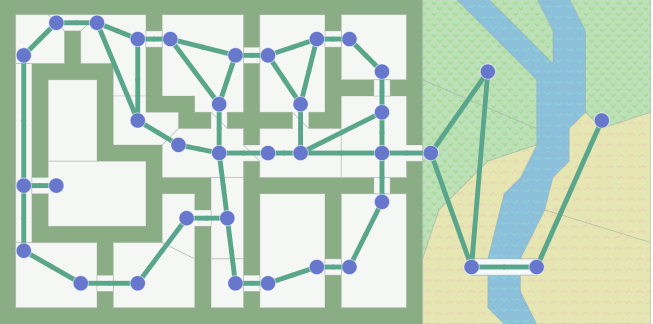
- 반대로, Grid와 같은 형태로 넣는다면? 이는 또 아래와 같습니다.

- 경로를 찾기 위한 Graph는 게임 내부에서 사용하는 지도와 꼭 같을 필요는 없습니다.
- Grid를 사용하는 게임 지도는 그리드를 사용하지 않는 Graph가 될 수 있고, 반대도 가능합니다.
A*는 가장 적은 Node로 가장 빠르게 실행됩니다.- Grid map은 결과로 나온 경로를 활용하기는 쉽지만, 많은 Node를 사용해야합니다.
- 이에 따라,
A*의 입력으로 넣는 지도를 잘 선택하는 것이 성능에 영향을 미치게 될 것입니다.
- 이 후부터는
A*의 입력으로 Grid map을 사용할 것이며, 이를 통해 컨셉을 더 명확하게 보여줄 수 있습니다.
Graph 탐색 알고리즘
- Graph에서 동작하는 알고리즘은 매우 많지만, 그 중 대표적인 것은 다음과 같습니다.
- BFS (Breadth First Search)
- 모든 방향에 대해 동일하게 탐색합니다.
- 일반적인 경로 탐색, 순차 지도 생성, 유체장 경로 탐색, 거리 지도, 다른 종류의 지도 분석 등에서도 유용하게 사용됩니다.
- Dijkstra (Uniform Cost Search)
- 탐색할 경로의 우선 순위를 지정해줍니다.
- 모든 경로를 탐색하는 대신, 가장 적은 비용의 경로를 우선 탐색합니다.
- 각 경로에 대해 비용을 적절히 할당하여, 낮은 비용을 경로를 따라가도록 할 수 있습니다.
- 도로를 따라가는 길에는 낮은 비용을
- 울창한 숲, 적군이 있는 도로 등에는 높은 비용을 할당하는 것입니다.
- 각 움직임에 대한 비용이 달라질 때,
BFS대신 사용할 수 있습니다.
- A*
Dijkstra을 하나의 경로를 찾는 것에 최적화 시킨 변형판입니다.Dijkstra은 모든 위치로 가는 경로를 찾지만, A*는 하나의 위치로 가거나, 몇몇 위치 중 가장 가까운 위치를 찾습니다.A*는 목표에 더 가까이 가는 것처럼 보이는 경로의 우선 순위를 매깁니다.
- 우선 가장 간단한
BFS부터 확인 후, 하나의 특징을 추가한 후, A*로 넘어가겠습니다.
Breadth First Search
- 이와 같은 알고리즘의 핵심 아이디어는
frontier라고 불리는 확대되는 링을 추적하는 것입니다.
- Grid에서 이와 같은 프로세스는
flood fill이라고 불립니다.
- Grid가 아닌 경우에도 동일한 기술은 사용할 수 있습니다.
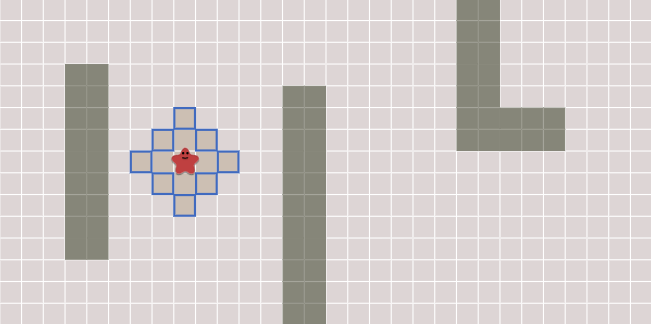
- 구현 방법은 다음과 같습니다.
- 시작 위치를 첫
frontier로 설정합니다.
- 아래의 과정을 반복합니다.
frontier에서 하나를 꺼냅니다.frontier에 인접한 곳을 살펴 이동 가능한 영역 중 확인하지 않은 곳을 frontier에 넣습니다.frontier에 인접한 곳이 없거나, 이동 가능한 영역이 없을 때까지 확인합니다.
- 여기서
frontier가 일반적인 BFS의 Queue를 의미합니다.
from queue import Queue를 사용하는 방법
frontier = Queue()
frontier.put(start) # 시작 위치를 frontier에 넣기
reached = set() # 방문 여부를 저장하기 위한 set
reached.add(start) # 시작 위치를 방문으로 표시
while not frontier.empty(): # frontier에 아무 것도 없을 때까지 반복
current = frontier.get() # frontier에서 하나 꺼내기
for next in graph.neighbors(current): # frontier에 인접한 위치 중
if next not in reached: # 방문하지 않은 곳이 있을 때
frontier.put(next) # 해당 위치를 frontier에 넣고
reached.add(next) # 방문 처리하기
from collections import deque을 사용하는 방법
frontier = deque()
frontier.append(start) # 시작 위치를 frontier에 넣기
reached = set() # 방문 여부를 저장하기 위한 set
reached.add(start) # 시작 위치를 방문으로 표시
while frontier: # frontier에 아무 것도 없을 때까지 반복
current = frontier.popleft() # frontier에서 하나 꺼내기
for next in graph.neighbors(current): # frontier에 인접한 위치 중
if next not in reached: # 방문하지 않은 곳이 있을 때
frontier.append(next) # 해당 위치를 frontier에 넣고
reached.add(next) # 방문 처리하기
- 이와 같은 반복은
A*를 포함한 Graph 탐색 알고리즘의 본질입니다.
- Graph 탐색은 지도 상에 있는 모든 위치를 어떻게 방문하는 지를 알려줄 뿐, 어떻게 최단 경로를 찾는 지는 알려주지 않습니다.
- 최단 경로를 찾기 위해서는 약간의 수정이 필요합니다.
- 우선 모든 위치에 대해 어디서부터 이동을 해서 왔는지를 저장해야 합니다.
- 그리고
reached set 대신, came_from dict를 사용할 것입니다.
frontier = Queue()
frontiner.put(start)
came_from = dict() # Path A --> B 는 came_from[B] = A로 저장될 것입니다.
came_from[start] = None
while not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next no in came_from:
frontier.put(next)
came_from[next] = current
- 이와 같이 수정하면,
came_from에 어디서부터 이동했는 지에 대한 내용이 저장됩니다.
- 이는 사이트의 이동 경로와 같습니다.
- 도착 위치로 부터 역순으로 시작 위치까지 돌아가면, 경로를 생성할 수 있습니다.
- 경로 생성을 위한 코드는 다음과 같습니다.
current = goal # 목표 장소를 시작 장소로 지정
path = [] # 역순으로 돌아오는 내용을 저장할 변수
while current != start: # 현재 위치가 출발 위치일 때까지 수행
path.append(current) # 현재 위치를 경로에 추가
current = came_from[current] # 현재 위치 이동 전의 위치로 이동
path.append(start) # 시작 위치를 포함시키기 위한 부분
path.reverse() # 시작 ~ 도착으로 경로 순서를 변경
- 이와 같은 경로 탐색 알고리즘은 Grid map 뿐만 아니라, 다양한 Graph 구조에서 가장 단순하게 동작하는 알고리즘입니다.
- 이 외에도 Graph의
Node가 State를 의미하고, Edge가 State Transition을 의미할 때도 사용할 수 있습니다.
빠르게 탈출하기
- 이전 챕터에서, 하나의 위치에서 모든 위치로 가는 경로를 모두 찾았습니다.
- 대부분의 경우, 하나의 위치로 가는 경로만 필요한 경우가 많습니다.
- 이와 같은 경우,
frontier를 확장하면서, 목적지가 발견되면 확장을 멈출 수 있습니다.
- 코드는 다음과 같습니다.
frontier = Queue()
frontier.put(start)
came_from = dict()
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal: # 확인하는 위치가 목표 장소이면 빠르게 탈출!
break
for next in graph.neighbor(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
이동 비용 고려하기
- 이전 챕터까지, 우리는 이동 비용이 모두 동일한 경우를 고려했습니다.
- 하지만, 몇몇 경우에는 각각의 움직임에 대한 다른 비용을 가지는 경우도 있습니다.
- 문명과 같은 게임에서, 평지나 사막을 따라 움직일 때는 비용이 1이지만, 숲이나 언덕은 비용이 5입니다.
- 아래의 지도에서 물을 건너 가는 것은 풀밭을 지나는 것에 비해 10배 큰 비용이 듭니다.

- 다른 예시는 대각선 이동이 축방향에 대한 이동(x, y)보다 비용이 큰 경우입니다.
- 우리는 이와 같은 비용들을 고려해서 경로를 찾고 싶습니다.
- 비용이 동일할 때와 다를 때의 경로의 차이를 확인하면 다음과 같이 확인할 수 있습니다.
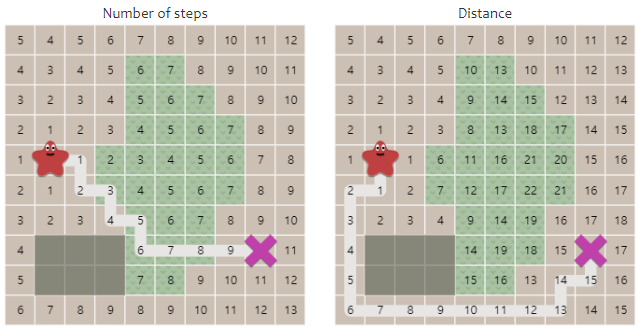
- 이와 같은 문제를 해결하기 위해,
Dijkstra 알고리즘(Uniform Cost Search)을 사용할 수 있습니다.
- 우선 전체 이동 비용을 고려하기 위한 변수인
cost_so_far을 추가하겠습니다.
- 도착 장소에 대한 평가를 하기 위해 이동 비용을 고려하고 싶습니다.
- 이를 위해,
Queue대신, Priority Queue를 사용합니다.
- 추가적으로, 비용이 다른 여러 장소에서 한 장소로 방문할 수 있기에 로직을 약간 변경합니다.
- 장소에 방문한 적이 없으면
frontier에 추가하는 방법 대신, 특정 장소까지의 새로운 경로가 이전까지의 최적 경로보다 좋은 경우에 frontier에 추가하겠습니다.
from queue import PriorityQueue를 사용한 구현
frontier = PriorityQueue()
frontier.put(strat, 0)
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current = goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put(next, priority)
came_from[next] = current
frontier = []
heapq.heappush(frontier, (0, start))
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0
while frontier:
(_, current) = heapq.heappop(frontier)
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
heapq.heappush(frontier, (priority, next))
came_from[next] = current
Queue를 Priority Queue로 변경한 결과, frontier가 확장하는 방법이 달라졌습니다.- 등고선을 통해 이러한 확장 방법을 확인할 수 있습니다.
- 숲에서는 확장이 느리며, 이를 통해, 숲을 가로질러 가는 방법이 아닌 다른 방법으로 최단 경로를 찾을 수 있습니다.
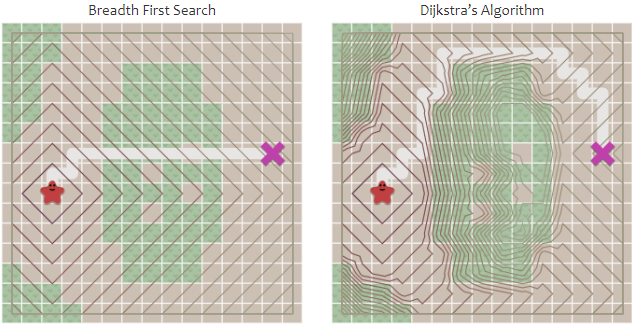
- 비용이 모두 동일하지 않은 형태의 Graph를 통해, Grid map 이외의 다양한 Graph를 탐색할 수 있습니다.
- 아래의 지도에서 이동 비용은 단순히 방과 방 사이를 이동하는 것에 기반하였습니다.
- 하지만 이동 비용은 특정한 영역을 피하거나, 특정한 영역을 선호하는 경로 생성에 사용할 수 있습니다.

Heuristic search
BFS와 Dijkstra에서는 frontier가 모든 방향으로 확장했습니다.- 이와 같은 방법은 모든 장소 또는 많은 장소에 대한 경로 찾기에는 매우 적합합니다.
- 하지만 가장 일반적인 경우는 하나의 위치에서 다른 하나의 위치로의 경로를 찾는 것입니다.
- 그렇다면,
frontier가 목표 장소 방향으로 우선적으로 확장되도록 해보겠습니다.
- 가장 먼저 할 일은 현재 위치가 목표 장소와 얼마나 가까운지 확인하는
heuristic 함수를 정의하는 것입니다.
def heuristic(start, goal):
# 사각형 그리드 맵에서의 맨해튼 거리를 반환
return abs(start.x - goal.x) + abs(start.y - goal.y)
Dijkstra에서는 시작 위치에서의 실제 거리를 기반으로 Priority Queue를 정렬하였습니다.- 대신,
Greedy Best First Search에서는 목표 장소까지의 예측 거리를 기반으로 Priority Queue를 정렬합니다.
- 따라서, 목표 장소에 가장 가까운 장소부터 탐색이 시작됩니다.
- 실제 코드는
Dijkstra와 거의 유사하며, cost_so_far를 사용하지 않습니다.
frontier = PriorityQueue()
frontier.put((0, start))
came_from = dict()
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
priority = heuristic(goal, next)
frontier.put((priority, next))
came_from[next] = current
- 결과는 다음과 같습니다.
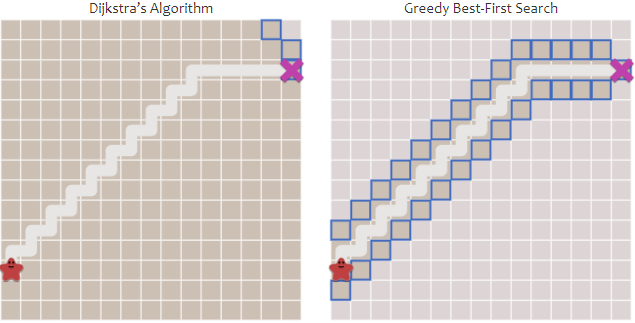
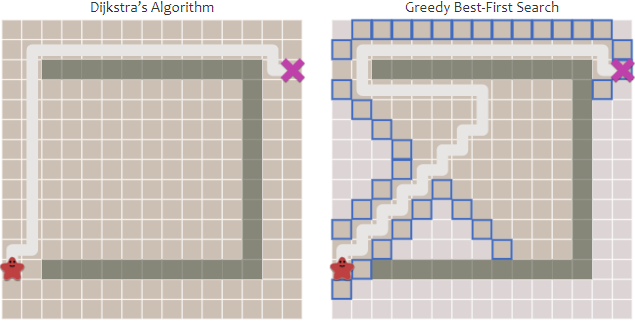
- 장애물이 없는 경우, 아주 빠르게 탐색이 완료됩니다.
- 반면, 장애물이 있는 경우, 탐색은 상대적으로 빠르지만, 경로가 최단거리가 아닙니다.
- 따라서
Greedy Best First Search 장애물이 별로 없는 경우 아주 빠르게 동작하지만, 경로가 좋지않을 수 있습니다.
- 조금 더 수정해서, 경로도 좋게 만들어봅시다!
A* Algorithm
Dijkstra 알고리즘
- 최단 경로를 찾는데 아주 적합합니다.
- 하지만, 가능성이 별로 없는 방향을 탐색하는 것을 통해 시간 낭비가 심한 편입니다.
Greedy Best First Search 알고리즘
- 가능성이 있는 방향을 우선적으로 탐색합니다.
- 하지만, 최단 경로를 찾지 못할 수 있습니다.
A* 알고리즘
- 위 두 가지의 장점을 결합합니다.
- 시작 위치에서의 실제 거리와 목표 장소까지의 예측 거리를 모두 적용하였습니다.
- 코드는
Dijkstra 알고리즘과 유사합니다.
frontier = PriorityQueue()
frontier.put((0, start))
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0
while not frotier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put((priority, next))
came_from[next] = current
Dijkstra는 시작 위치에서의 거리만을 비교하였습니다.Greedy Best First Search는 도착 장소까지의 예측 거리만을 비교하였습니다.A*는 두 거리의 합을 이용하였습니다.- 결과를 비교하면, 다음과 같습니다.
A*와 Dijkstra는 둘 다, 최적의 경로를 찾을 수 있습니다.- 하지만
A*는 Dijkstra보다 빠릅니다.
Greedy Best First Search는 A*보다 빠를 수 있습니다.- 하지만
Greedy Best First Search는 최적의 경로를 찾을 수 없을 수도 있습니다.
결론
- 모든 위치에 대한 경로를 찾아야하며, 모든 이동 비용이 동일하다면
BFS
- 모든 위치에 대한 경로를 찾아야하며, 모든 이동 비용이 동일하지 않다면
Dijkstra
- 한 장소에 대한 경로를 찾아야하거나, 몇 개의 장소 중 가장 가까운 장소를 찾아야한다면
Greedy Best First Search or A*
- 대부분의 경우
A*의 성능이 Greedy Best First Search보다 좋습니다.
- 만약
Greedy Best First Search를 사용하고 싶은 경우, A*를 inadmissible heuristic과 함께 사용하는 것을 고려해보십시오.
A*를 inadmissible heuristic과 함께 사용하게 되면, 최적의 해를 못찾을 수도 있기 때문을 말하는 것 같음Heuristic 함수가 실제 해답에 해당하는 거리보다 짧을 경우, A*는 최적의 해를 찾을 수 있습니다.Heuristic 함수의 값이 작아지면, A*는 Dijkstra와 유사해집니다.Heuristic 함수의 값이 커지면, A*는 Greedy Best First Search와 유사해집니다.- 비용 측면에서는 가장 우선적으로 해야할 일은 Graph의 쓸모 없는 장소를 지우는 것입니다.
- Graph의 크기를 줄이는 것이 Graph 탐색 알고리즘을 빠르게 할 수 있습니다.
A*는 단순히 그래프 탐색에 사용될 수 있으며 아래의 내용을 고려하지는 않습니다.
- 장애물 회피
- 지도의 변경
- 위험 지역의 평가
- 회전 반경
- 물체의 크기
- 경로의 부드러움 등
Review
- 2D Occupancy Grid Map의 경로 찾는 알고리즘의 원리를 이해할 수 있었다.
- 기존에 배웠던
BFS, Dijkstra, A*의 변환되는 과정을 보니 이해하기가 더 좋았던 것 같다.
- Graph의 Edge 비용을 조절하여, 경로 탐색에 대한 기준을 설정할 수 있다는 사실을 알게 되었다.
- Grid Map의 각 Cell을 Node로 변경합니다.
- 각 Cell의 인접 상태(상하좌우 or 상하좌우대각)를 이용하여 Edge로 연결합니다.
all_nodes = []
for x in range(map_size.x):
for y in range(map_size.y):
all_nodes.append([x, y])
def neighbor(node):
dirs = [[1, 0], [0, 1], [-1, 0], [0, -1]] # 상하좌우
# dirs = [[1, 0], [0, 1], [-1, 0], [0, -1], [1, 1], [1, -1], [-1, -1], [-1, 1]] # 상하좌우대각
result = []
for dir in dirs:
neighbor = [node[0] + dir[0], node[1] + dir[1]]
if neighbor in all_nodes:
result.append(neighbor)
return result
- 이 외의 고려할 사항
- 방향 그래프 (일방 통행인 경우)
- 멀티 그래프 (가는 방법이 여러 가지인 경우)
- 이동 비용이 다른 경우 (위험한 영역 또는 험한 지역 등)
- 장애물에 대한 처리
- 장애물로 표시된 Node를
all_node에서 지우는 방법
- 장애물로 표시된 Node와 연결된 Edge를 지우는 방법
- 장애물로 표시된 Node와 연결된 Edge의 비용을 $\infty$로 바꾸는 방법
- 마지막 방법은 그래프 생성 후, 장애물의 위치 변경이 필요할 때 사용하면 좋다
구현
- Grid Map 기반의
BFS, Dijkstra, Greedy Best First Search, A* 구현
- Implementation of A*
- 일반적인 Graph에서
BFS 및 Dijkstra의 차이 및 속도를 확인해보았다.
- 확인해보니
deque, heapq가 Queue, PriorityQueue보다 훨씬 빠르더라..
- 이유를 찾아보니
Queue랑 PriorityQueue는 Thread-Safe해서 그만큼 시간이 더 오래걸린다고 한다.
- 단일 스레드에서는
deque, heapq가 좋고 멀티 스레딩에서는 Queue, PriorityQueue를 쓰면 된다고 한다.
- Grid Map은 추후에 해보겠습니다.
from queue import Queue, PriorityQueue
from collections import deque
import heapq
import time
def time_check_decorator(func):
def decorated(*args, **kwargs):
ref_time = time.time()
func(*args, **kwargs)
print(f'time : {time.time() - ref_time:.7f}s')
return decorated
class normal_graph():
def __init__(self, _node_num):
self.edge = [[] for _ in range(_node_num + 1)]
def add(self, _start, _end, _cost):
self.edge[_start].append((_end, _cost))
def neighbors(self, _position):
result = []
for end, cost in self.edge[_position]:
result.append(end)
return result
def cost(self, _start, _next):
for end, cost in self.edge[_start]:
if end == _next:
return cost
def print_graph(self):
print(self.edge)
graph = normal_graph(6)
graph.add(1, 2, 2)
graph.add(1, 3, 5)
graph.add(1, 4, 1)
graph.add(2, 3, 3)
graph.add(2, 4, 2)
graph.add(3, 2, 3)
graph.add(3, 6, 5)
graph.add(4, 5, 1)
graph.add(4, 3, 3)
graph.add(5, 3, 1)
graph.add(5, 6, 2)
graph.print_graph()
start = 1
goal = 6
# BFS Queue
@ time_check_decorator
def BFS_using_Queue(graph):
frontier = Queue()
frontier.put(start)
came_from = dict()
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
current = goal # 목표 장소를 시작 장소로 지정
path = [] # 역순으로 돌아오는 내용을 저장할 변수
while current != start: # 현재 위치가 출발 위치일 때까지 수행
path.append(current) # 현재 위치를 경로에 추가
current = came_from[current] # 현재 위치 이동 전의 위치로 이동
path.append(start) # 시작 위치를 포함시키기 위한 부분
path.reverse() # 시작 ~ 도착으로 경로 순서를 변경
print("BFS Queue Path = {}".format(path))
# BFS deque
@ time_check_decorator
def BFS_using_deque(graph):
frontier = deque()
frontier.append(start)
came_from = dict()
came_from[start] = None
while frontier:
current = frontier.popleft()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
frontier.append(next)
came_from[next] = current
current = goal # 목표 장소를 시작 장소로 지정
path = [] # 역순으로 돌아오는 내용을 저장할 변수
while current != start: # 현재 위치가 출발 위치일 때까지 수행
path.append(current) # 현재 위치를 경로에 추가
current = came_from[current] # 현재 위치 이동 전의 위치로 이동
path.append(start) # 시작 위치를 포함시키기 위한 부분
path.reverse() # 시작 ~ 도착으로 경로 순서를 변경
print("BFS deque Path = {}".format(path))
# Dijkstra PriorityQueue
@ time_check_decorator
def Dijkstra_using_PriorityQueue(graph):
frontier = PriorityQueue()
frontier.put((0, start))
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
(_, current) = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put((priority, next))
came_from[next] = current
current = goal # 목표 장소를 시작 장소로 지정
path = [] # 역순으로 돌아오는 내용을 저장할 변수
while current != start: # 현재 위치가 출발 위치일 때까지 수행
path.append(current) # 현재 위치를 경로에 추가
current = came_from[current] # 현재 위치 이동 전의 위치로 이동
path.append(start) # 시작 위치를 포함시키기 위한 부분
path.reverse() # 시작 ~ 도착으로 경로 순서를 변경
print("Dijkstra Path = {}".format(path))
# Dijkstra heapq
@ time_check_decorator
def Dijkstra_using_heapq(graph):
frontier = []
heapq.heappush(frontier, (0, start))
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0
while frontier:
(_, current) = heapq.heappop(frontier)
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
heapq.heappush(frontier, (priority, next))
came_from[next] = current
current = goal # 목표 장소를 시작 장소로 지정
path = [] # 역순으로 돌아오는 내용을 저장할 변수
while current != start: # 현재 위치가 출발 위치일 때까지 수행
path.append(current) # 현재 위치를 경로에 추가
current = came_from[current] # 현재 위치 이동 전의 위치로 이동
path.append(start) # 시작 위치를 포함시키기 위한 부분
path.reverse() # 시작 ~ 도착으로 경로 순서를 변경
print("Dijkstra Path = {}".format(path))
BFS_using_Queue(graph)
BFS_using_deque(graph)
Dijkstra_using_PriorityQueue(graph)
Dijkstra_using_heapq(graph)












